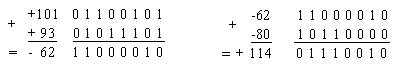C0-Révision (Structure machine)

CHAP 0                                                                  Révision: 

I. Systèmes de numération

1. Introduction :

  Depuis le début des temps, des dizaines de systèmes de numération ont été créés pour répondre à des besoins de mesures de quantité et de grandeur. On raconte, qu'avant l'avènement d’un système de numération, un berger se servait de cailloux pour compter les moutons. C'est à partir de besoins de cette nature que les systèmes de numération ont été inventés. 

  Notre système de numération repose essentiellement sur la base 10 (surement à cause des 10 doigts des deux mains). On trouve aussi un certain nombre d'occurrences de nombres exprimés dans d'autres systèmes de notation, telle que la base 60 pour compter les secondes et les minutes, la base 12 pour compter les heures, etc. 

  L'ordinateur a 2 états significatifs (impulsion électriques). Le système de numération qu'il emploie est donc le système binaire. Il est donc nécessaire de développer des techniques de conversions de notation afin de pouvoir transcrire des nombres d'un système de notation dans un autre. A titre d'exemple, les ordinateurs actuels convertissent constamment les nombres représentés en base 10 vers un système en base 2.

  Ce paragraphe présente, quelques méthodes de conversion, nous utiliserons les bases 2, 8,10 et16.

2. Généralités. 

Définition : Une base est le nombre par lequel on doit multiplier une unité pour passer d’un ordre au suivant. C’est le nombre qui sert à définir un système de numération. La base du système décimal est 10 alors que celle du système octal est 8. 

  D'une manière générale, le nombre anan-1...a2a1a0 si il est exprimé en base b ne pourra comporter que des chiffres ai compris entre 0 et b-1. Notons ai la suite des chiffres utilisés pour écrire un nombre x = an an-1 ... a1 a0      → a0 est le chiffre des unités.

• En décimal, b=10, ai ∈ { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };
• En binaire, b=2, ai ∈ { 0, 1 } : 2 chiffres binaires, ou bits;En Octal ; b = 8; ai ∈ { 0, 1, 2, 3, 4, 5, 6, 7};
• En hexadécimal, b=16, ai ∈ { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F } (on utilise les 6 premières lettres comme des chiffres).

La notation ( )b indique que le nombre est écrit en base b. Nous utiliseront aussi les lettres B, ∅, H à la fin d’un nombre écrit en binaire, en octale ou en hexadécimal.

3. Ecriture des nombres entiers

  En base 10, on écrit par exemple 1986 pour représenter le nombre 1986 = 1*10^3 + 9*10^2 + 8*10^1 + 6*10^0

  Dans le cas général, en base b, le nombre représenté par une suite de chiffres anan-1...a2a1a0 est donné par: an * b^n + an-1 * b^n-1 + ... + a2 * b^2 + a1 * b + a0 calculée en base 10. a0 est le chiffre de poids faible, et an le chiffre de poids fort. 
  Exemple: ( 101101 )2 = 1*2^5+0*2^4+1*2^3+1*2^2+0*2^1+1*2^0=32+8+4+0+1 = 45 
                      (6172)8 = 6*8^3 + 1*8^2 + 7*8 + 2 = 3194 
                 (7A8BD)16 = 7*16^4 +10*16^3 +8*16^2 +11*16 +13 = 501949^
 Remarque: Dans un système à base b et sur n positions. On peut représenter les nombres de 0 à (b^n -1)

4. Ecriture des nombres fractionnaires 

  Les nombres fractionnaires sont ceux qui comportent des chiffres après la virgule. Dans le système décimal, on écrit par exemple: 

  12,346 = 1*10^1 + 2*10^0 + 3*10^-1 + 4*10^-2 + 6*10^-3 

En général, en base b, on écrit:

an an-1 ... a1 a0, a-1 a-2 ... a-p = an b^n + an-1b^(n-1) + ... + a0 b^0 + a-1 b^-1 + ... + a-p b^-p

Exemple:

     (11,1011)2 = 1*2+1+ 1* 2^-1 + 0 *2^-2 + 1 * 2^-3 + 1* 2^-4 = 3 + (1011)2 /2^4 = 3.6875

5. Opérations arithmétiques

  Les opérations arithmétiques s'effectuent en base quelconque b avec les mêmes méthodes qu'en base 10. Une retenue ou un report apparaît lorsque l'on atteint ou dépasse la valeur b de la base.

6. Passage d'une base quelconque à la base 10

  En exposant les principes des systèmes de numération de position, nous avons déjà vu comment convertir les nombres de base 8, base 2 et base 16 en nombres décimaux. 

  Exemple en hexadécimal: (AB)16 = 10*16^1 + 11*16^0 =160 + 11 = 171

7. Passage de la base 10 vers une base quelconque

•  Nombres entiers On procède par divisions successives. On divise le nombre par la base, puis le quotient obtenu par la base, et ainsi de suite jusqu’à obtention d'un quotient nul.

La suite des restes obtenus correspond aux chiffres dans la base visée, a0 a1 ... an.

  Exemple:   44 = ( ? )2.

                    44 ÷ 2 = 22 reste 0    a0 = 0 

                    22 ÷ 2 = 11 reste 0    a1 = 0 

                    11 ÷ 2 = 5 reste 1      a2 = 1 

                      5 ÷ 2 = 2 reste 1      a3 = 1 

                      2 ÷ 2 = 1 reste 0      a4 = 0

                      1 ÷ 2 = 0 reste 1      a5 = 1   Donc 44 = (101100)2.

• Nombres fractionnaires On multiplie la partie fractionnaire par la base en répétant l'opération sur la partie fractionnaire du produit jusqu'a ce qu'elle soit nulle (ou que la précision voulue soit atteinte). Pour la partie entière, on procède par divisions comme pour un entier. 

  Exemple: conversion de 54,25 en base 2 Partie entière: 54 = (110110)2 par divisions.

  Partie fractionnaire:

                                    ➡  0,25 * 2 = 0,5      →     a-1 = 0

                                         0,5 * 2  = 1,0       →     a-2 = 1

                                         0,0 * 2  = 0,0       →     a-3 = 0 donc 54,25 = (110110.01)2

                                    ➡  0.6 = ( ? )16

                                         0,6 * 16 = 9,6       →     a-1 = 9

                                         0,6 * 16 = 9,6       →     a-2 = 9

                                         . . . . . . . . . . 

                                                                          Donc   0,6 = (0,99999...)16

• Cas des bases 2, 8 et 16

  Ces bases correspondent à des puissances de 2 (2^1, 2^3 et 2^4), d'où des passages de l'une à l'autre très simples. Les bases 8 et 16 sont pour cela très utilisées en informatique, elles permettent de représenter rapidement et de manière compacte des configurations binaires. La base 8 est appelée notation octale, et la base 16 notation hexadécimale. Chaque chiffre en base 16 (2^4) représente un paquet de 4 bits consécutifs. 

  Par exemple: (1010011011)2 = (0010 1001 1011)2 = (29B)16

  De même, chaque chiffre octal représente 3 bits. 

                           (10 011 000 111 110)2 = (23076)8

II. Codage de données

1. Introduction

  Les informations traitées par un ordinateur peuvent être de différents types (texte, nombres, etc.) mais elles sont toujours représentées et manipulées par l'ordinateur sous forme binaire. Toute information sera traitée comme une suite de 0 et de 1. 

  Le codage d'une information consiste à établir une correspondance entre la représentation externe (habituelle) de l'information (le caractère A ou le nombre 36 par exemple), et sa représentation interne dans la machine, qui est une suite de bits. On utilise la représentation binaire car elle est simple, facile à réaliser techniquement.

Le Bit : Bit signifie "binary digit", c'est-à-dire 0 ou 1 en numérotation binaire. C'est la plus petite unité d'information manipulable par une machine. 

  On peut le représenter physiquement:

• par une impulsion électrique qui correspond à la valeur 1 ou une absence d'impulsion qui correspond à la valeur 0.
• par des alvéoles ou des espaces dans une surface (CD-ROM)
• grâce à des bistables, c'est-à-dire des composants qui ont deux états d'équilibre (un correspond à l'état 1, l'autre à 0)

Avec un bit on peut avoir deux états différents : soit 1, soit 0. 

Avec 2 bits on peut avoir quatre états différents (2*2): 00, 01, 10, 11 

Avec 3 bits on peut avoir huit états différents (2*2*2): 000, 001, 010, 011, 100, 101, 110, 111

Avec 8 bits on a 2*2*2*2*2*2*2*2=256 possibilités, c'est ce que l'on appelle un octet. 

  Cette notion peut être étendue à n bits : on a alors 2^n possibilités.

L'octet: Octet est une unité d'information composée de 8 bits. Il permet de stocker un caractère, tel qu'une lettre, un chiffre ...

• Un kilo-octet (Ko) ne vaut pas 1000 octets mais 2^10 octets = 1024 octets
• Un méga-octet (Mo) vaut 2^10 Ko = 1024 Ko = 2^20 octets = 1 048 576 octets
• Un giga-octets (Go) vaut 2^10 Mo = 1024 Mo = 2^30 octets = 1 073 741 824 octets
• Un téra-octet (To) vaut 2^10 Go = 1024 Go = 2^40 octets = 1 099 511 627 776 octets

Les octets sont regroupés en mot-mémoire. La longueur d'un mot-mémoire varie d'une machine à l'autre (8, 16, 24, 32, 64 bits) la longueur des mot-mémoires est une caractéristique importante dans l'architecture d'un ordinateur.

2. Codification des nombres entiers

  La représentation (ou codification) des nombres est nécessaire afin de les stocker et manipuler par un ordinateur. Le principal problème est la limitation de la taille du codage: un nombre mathématique peut prendre des valeurs arbitrairement grandes, tandis que le codage dans l'ordinateur doit s'effectuer sur un nombre de bits fixé.

Entiers naturels (non signés)

  Les entiers naturels (positifs ou nuls) sont codés sur un nombre d'octets fixé (un octet est un groupe de 8 bits). On rencontre habituellement des codages sur 1, 2 ou 4 octets, plus rarement sur 64 bits (8 octets, par exemple sur les processeurs DEC Alpha). 

  Un codage sur n bits permet de représenter tous les nombres naturels compris entre 0 et 2^n-1. Par exemple sur 1 octet, on pourra coder les nombres de 0 à 255 = 2^8-1. 

  On représente le nombre en base 2 et on range les bits dans les cellules binaires correspondant à leur poids binaire, de la droite vers la gauche. Si nécessaire, on complète à gauche par des zéros (bits de poids fort).

Entiers relatifs (signés)

  Il faut ici coder le signe du nombre. On utilise le codage en complément à deux qui permet d'effectuer ensuite les opérations arithmétiques entre nombres relatifs de la même façon qu'entre nombres naturels.

1. Entiers positifs ou nuls: On représente le nombre en base 2 et on range les bits comme pour les entiers naturels. Cependant, la cellule de poids fort est toujours à 0: on utilise donc n-1 bits. , qui permet d'effec-tuer ensuite les opérations arithmétiques entre nombres relatifs de la même façon qu'entre nombres naturels. Le plus grand entier positif représentable sur n bits en relatif est donc 2^(n-1) - 1.

2. Entiers négatifs: Soit x un entier positif ou nul représenté en base 2 sur n-1 bits.  La représentation de -x est obtenue par (-x) + (x) = 2^n, on dit complément vrai (à deux). Pour obtenir le codage d'un nombre x négatif, on code en binaire sa valeur absolue sur n-1 bits, puis on complémente (inverse) tous les bits et on ajoute 1.

Exemple: soit à coder la valeur -2 sur 8 bits. On exprime 2 en binaire, soit 00000010. On inverse les bits On obtient 11111101. On ajoute 1 et on a le résultat: 1111 1110. 

Remarques:

1. le bit de poids fort d'un nombre négatif est toujours 1;
2. sur n bits, le plus grand entier positif est: 2^(n-1) - 1 = 0111…1;
3. sur n bits, le plus petit entier négatif est :     -2^(n-1) = 1000 …0;

Sur 8 bits on peut donc représenter les nombres:

Opération arithmétique et débordement (Overflow):

  Les opérations d’additions et de soustractions se déroulent normalement comme en binaire. Il y a débordement si le résultat n’appartient pas à l’intervalle des entiers représentables. Le débordement peut être détecté:

• en comparant le signe des opérandes au signe du résultat: s'il y a contradiction, il y a débordement, ou
• en comparant la retenue entrante dans le bit de poids fort avec la retenue sortante : s'ils sont différents, il y a débordement.

Exemple:

3. Représentation des nombres réels (norme IEEE)

Plusieurs représentations possibles :

• virgule fixe : revient à manipuler des entiers (caisses enregistreuses)
• couple (numérateur, dénominateur): représentation juste uniquement pour les nombres rationnels
• virgule flottante

Virgule flottante

  Un nombre réel x = ± m* b^e est représenté par un signe, une mantisse m, un exposant e, et une base b. Il existe une infinité de représentation du même nombre. 

  Représentation normalisée : pour une base b, la mantisse est prise dans l'intervalle [1, b[ (zéro admet une représentation particulière). 

  La précision et l'intervalle de valeurs représentées dépendent du nombre de bits utilisés pour coder la mantisse et l'exposant.

Norme IEEE754:  La norme IEEE 754 est la norme la plus utilisée pour représenter les réels.

• nombres codés sur 32 bits (simple précision), ou 64 bits (double précision)

• la mantisse appartient à l'intervalle [1,0          10,0[ (en binaire)

• le seul chiffre à gauche de la virgule étant toujours 1, n'est pas représenté

• l'exposant E du nombre est codé avec un excès de 127 (simple précision) ou 1023 (double précision) (i.e. E = e+127 ou E = e+1023)

Sur 32 bits :

Exemple: Coder le nombre réel 95.7 selon la norme IEEE 754 

Solution: 95.7 = 1011111,101100100010001000100010001000100…B=1,01111110110010001000100 B * 2^6 

E = 6 + 127 = 128 + 5 = 10000101B 

95.7 est codé par: 0 :100 00101 : 01111110110 0100 0100 0100 

Précision: La représentation des nombres réels sur une machine se base sur un nombre fini de valeurs. C'est donc une représentation approchée. 

  Précision de la représentation = différence entre les mantisses de deux nombres réels consécutifs. 

! La précision ne dépend que de la mantisse.

Remarques: En conséquence de ces limites, il existe donc un nombre limité de nombres représentables sur machine.

1. Le zéro : le zéro est le seul nombre qui ne peut pas se représenter dans le système en virgule flottante à cause de la contrainte de non nullité du premier digit.
2. Les exposants 00000000 et 11111111 sont interdits:
   • l'exposant 00000000 signifie que le nombre est dénormalisé; 
   • l'exposant 11111111 indique que l'on n'a pas affaire à un nombre (on note cette configuration NaN, Not a Number, et on l'utilise pour signaler des erreurs de calculs, comme par exemple une division par 0).
3. Les plus petit exposant est donc -126, et le plus grand +127.
4. Dépassement de capacité : Si l'on cherche à représenter un nombre très petit, on produit un débordement par valeur inférieure (underflow). Si l'on cherche à représenter un nombre très grand, on produit un débordement par valeur supérieure (overflow).

4. Décimaux codés binaire

  Cette codification est utilisée souvent dans les calculatrices de poche et de bureau, Un nombre décimal, qui est composé d’un ou plusieurs chiffres (0 à 9), est toujours codé à l’aide de bits. Il existe un certain nombre de codes; voici deux.

• CODE DCB Décimal Codé Binaire : chaque chiffre d'un nombre est codé sur 4 bits Ce code simplifie la conversion décimal binaire.
  Pour l’addition, il faut ajouter 6 chaque fois que le résultat est >9.

• CODE Excédent-3: Chaque chiffre décimal d'un nombre est codé séparément en son équivalent binaire + 3.
  
    Exemple: 4850 est codé par 0111 1011 1000 0011
  

    Au cours d’une addition, le chiffre décimal est augmenté de 6; en lui retirant systématiquement 3, le résultat sera codé en code excédent-3. Si une addition de ce type conduit à une retenue du cinquième ordre binaire, il faudra au contraire ajouter 3 aux deux ordres décimaux pour que les chiffres correspondants se retrouvent en code excédent-3.

5. Représentation des caractères

  Les caractères sont des données non numériques: il n'y a pas de sens à additionner ou multiplier deux caractères. Par contre, il est souvent utile de comparer deux caractères, par exemple pour les trier dans l'ordre alphabétique.

 Les caractères, appelés symboles alphanumériques, incluent les lettres majuscules et minuscules, les symboles de ponctuation (& ~ , . ; # " - etc...), et les chiffres.

 Un texte, ou chaîne de caractères, sera représenté comme une suite de caractères.

 Le codage des caractères est fait par une table de correspondance indiquant la configuration binaire représentant chaque caractère. Les deux codes les plus connus sont l'EBCDIC (en voie de disparition) et le code ASCII (American Standard Code for Information Interchange). 

 Le code ASCII représente chaque caractère sur 7 bits (on parle parfois de code ASCII étendu, utilisant 8 bits pour coder des caractères supplémentaires).

 Notons que le code ASCII original, défini pour les besoins de l'informatique en langue anglaise) ne permet la représentation des caractère accentués (é, è, à, ù, ...), et encore moins des caractères chinois ou arabes. Pour ces langues, d'autres codages existent, utilisant 16 bits par caractères.

ASCII US défini par la norme iso-646

  Pour bien lire le tableau, il faut construire le code hexadécimal en prenant d'abord le digit de la ligne, puis le digit de la colonne. Par exemple, la lettre "n" a pour code hexadécimal 6E.

  Plusieurs points importants à propos du code ASCII:

• Les codes compris entre 0 et 31 ne représentent pas des caractères, ils ne sont pas affichables. Ces codes, souvent nommés caractères de contrôles
• Les lettres se suivent dans l'ordre alphabétique (codes 65 à 90 pour les majuscules, 97 à 122 pour les minuscules), ce qui simplifie les comparaisons. sont utilisés pour indiquer des actions comme passer à la ligne (CR, LF), émettre un bip sonore (BEL), etc.
• On passe des majuscules aux minuscules en modifiant le 5ième bit, ce qui revient à ajouter 32 au code ASCII décimal.
• Les chiffres sont rangés dans l'ordre croissant (codes 48 à 57), et les 4 bits de poids faibles définissent la valeur en binaire du chiffre.

III. Protection contre les erreurs

  1. Introduction :

  Le codage binaire est très pratique pour une utilisation dans des appareils électroniques tels qu'un ordinateur, dans lesquels l'information peut être codée grâce à la présence ou non d'un signal électrique. Toutefois, le signal électrique peut subir des perturbations, notamment lors du transport des données (dans un réseau par exemple) car les données circulent sur un long trajet. Ainsi, le contrôle de la validité des données est nécessaire pour certaines applications (professionnelles, bancaires, industrielles, confidentielles, relatives à la sécurité, ...). C'est pourquoi il existe des mécanismes permettant de garantir un certain niveau d'intégrité des données.

2. Le contrôle de parité

  La plupart des systèmes de contrôle d'erreur sont basés sur un ajout d'information permettant de vérifier la validité des données.

  Le contrôle de parité est un des systèmes de contrôle les plus simples. Il consiste à ajouter un bit supplémentaire (appelé bit de parité) à un certain nombre de bits de données généralement 7, pour former un octet avec le bit de parité) dont la valeur (0 ou 1) . la valeur est telle que le nombre total de bit à 1 (calculé sur m+1) est pair ou impair. Si la parité n’est plus respectée, l’erreur est détectée, mais s’il y a double erreur, la parité est aussi respectée et alors l’erreur n’est plus détectée.

3. Double parité:

  En plus du contrôle par octet (horizontal), on ajoute une parité par bit pour un bloc d’information (parité longitudinal). Ce double contrôle permet de détecter un nombre impair d’erreur et parfois de corriger certaines erreurs.

4. Le code de Hamming:

  Il est basé sur les tests de parité pair et ne permet de corriger qu’un bit en erreur.

Au m bits d’information, on ajoute k bits de contrôle. Pour que les bits de contrôle puissent coder les

m+k+1 possibilités d’erreurs (dont l’absence d’erreur) ,il faut que 2^k >= m+k+1. Les bits sont numérotés

de 1 à m+k et Les bits de test sont placés en position 1, 2, 4, 8, . . (puissance de 2). Chaque bit est contrôlé par les bits qui additionnés donnent le numéro de ce bit. Ainsi:

• Le bit 1 contrôle les bits 1, 3, 5, 7, 9, 11, 13, 15, 17,. . . . .
• Le bit 2 contrôle les bits 2, 3, 6, 7, 10, 11, 14, 15, . . . .
• Le bit 4 contrôle les bits 4, 5, 6, 7, 12, 13, 14, 15 . . . . .
• Le bit 8 contrôle les bits 8, 9, 10, 11, 12, 13, 14, 15, 24 . . .

  Exemple: Soit l’information composée de 8 bits m7,m6,m5, m4,m3,m2, m1,m0

  Il faut donc 4 bits de contrôle k3,k2, k1,k0 .

  L’information avec contrôle devient m7,m6,m5, m4, k3,m3,m2, m1, k2,m0, k1,k0

  Si L’information est: 10110101 Après L’ajout des bits de contrôle On obtient 101110100110

On suppose que le bit 10 est détérioré (inversé) lors d'une transmission, 100110100110 .

Après calcule des parités pour les bits de contrôle, on obtient 1010 = 2+8 = 10eme bit erroné.